Ajustement Linéaire

LEXIQUE :

Choisissez le terme à expliquer...

Ajustement affine de Y en X par la méthode des moindres carrés :

Etant donné un nuage de points :

il existe un modèle affine : Y = a X + b

rendant minimum la somme des carrés des résidus ( SCR ) :

Ce modèle s'obtient en prenant : a =

et en écrivant que la droite d'équation : y = a x + b passe par le point moyen du nuage : = a + b

Cov ( X , Y ) = ( x_i - ) ( y_i - )

est la covariance des variables X et Y tandis que :

s² ( X ) = ( x_i - )²

est la variance de la variable X.

Le modèle obtenu par cette méthode s'appelle l'ajustement affine de Y en X par la méthode des moindres carrés.

Ajustement exponentiel :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ), on dit que fest un modèle exponentiel ou un ajustement exponentiel de Y en X si la fonction f est de la forme :

f ( X ) = k a^X

Ajustement par une fonction puissance :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ),

on dit que f est un modèle par une fonction puissance si la fonction f est de la forme :

f ( X ) = k X^C

Coefficient de corrélation linéaire :

Etant donné une variable statistique réelle X prenant les n valeurs x₁, x₂, ... , x_n et une variable statistique réelle Y prenant les n valeurs y₁, y₂, ... , y_n, le nombre

s'appelle le coefficient de corrélation linéaire des variables X et Y.

Coefficient de détermination :

Etant donné une variable statistique réelle X prenant les n valeurs x₁, x₂, ... , x_n et une variable statistique réelle Y prenant les n valeurs y₁, y₂, ... , y_n, le nombre

s'appelle le coefficient de corrélation linéaire des variables X et Y.

Le nombre : R = r² =

s'appelle le coefficient de détermination des variables X et Y.

Coefficient directeur :

Etant donné une droite D et un repère orthonormé : R = ( O ; , ) du plan,

un vecteur directeur de D, α une mesure en radians de l'angle

le nombre tan α s'appelle le coefficient directeur de la droite D.

Si l'équation de la droite D dans le repère R est de la forme : y = a x + b

a est égal au coefficient directeur de la droite D.

Composante imprévisible :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

A toute valeur x_i de X est associée une valeur y_i relevée par l'observateur :

y_i est la valeur observée de la variable expliquée.

= f ( x_i ) est la valeur théorique ou valeur expliquée par le modèle.

e_i = y_i - est le résidu du modèle.

On dit aussi que :

est la composante prévisible par le modèle et

e_i la composante imprévisible.

Composante prévisible :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

A toute valeur x_i de X est associée une valeur = f ( x_i ).

est la valeur théorique ou valeur expliquée par le modèle.

On dit aussi que est la composante prévisible.

Covariance :

Etant donné une variable statistique réelle X prenant les n valeurs x₁, x₂ = , ... , x_n et une variable statistique réelle Y prenant les n valeurs y₁, y₂, ... , y_n, le nombre

Cov ( X , Y ) = ( x_i - ) ( y_i - )

est la covariance des variables X et Y. Pour calculer Cov ( X , Y ) on peut utiliser la formule :

Cov ( X , Y ) = -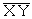

Direction de droites :

On considère une droite D. L'ensemble des droites parallèles à la droite D constitue une direction de droites.

Une direction de droites est caractérisée par la donnée d'un vecteur directeur d'une droite quelconque de la direction.

Etant donné un repère cartésien du plan, une direction de droite est également caractérisée par le coefficient directeur d'une droite quelconque de la direction.

Dispersion d'un nuage par rapport à une droite :

Etant donné un nuage de points et une droite D, on appelle dispersion du nuage par rapport à la droite D la racine carrée de la moyenne des carrés des distances euclidiennes des points du nuage à la droite D.

Distance euclidienne entre une droite D et un point :

Etant donné une droite D, un point M, et la direction orthogonale à D, si m est la projection de M sur D, la distance entre m et M représente la distance euclidienne entre la droite D et le point M.

Droite d'ajustement de X en Y :

Etant donné un nuage de points et la direction de l'axe des abscisses, il existe une droite D et une seule par rapport à laquelle l'éloignement du nuage dans la direction de l'axe des abscisses est minimum.

Cette droite D s'appelle la droite d'ajustement de X en Y du nuage.

Droite d'ajustement de Y en X :

Etant donné un nuage de points et la direction de l'axe des ordonnées, il existe une droite D et une seule par rapport à laquelle l'éloignement du nuage dans la direction de l'axe des ordonnées est minimum.

Cette droite D s'appelle la droite d'ajustement de Y en X du nuage.

Droite de régression orthogonale :

Etant donné un nuage de points, il existe une droite D et une seule par rapport à laquelle le moment d'inertie du nuage, ou ce qui est équivalent la dispersion du nuage, est minimum.

Cette droite s'appelle la droite de régression orthogonale du nuage.

Ecart à la moyenne :

Soit X une variable statistique réelle prenant les valeurs : x₁, x₂, ... , x_n et soit la moyenne arithmétique de ces valeurs.

On appelle écart à la moyenne les nombres :

x₁ - , x₂ - , ... , x_n -

(voir aussi valeurs centrées, variable statistique centrée).

Ecart des prévisions à la moyenne :

Etant donné un nuage de points :

un modèle affine : Y = a X + b ajusté à ce nuage par la méthode des moindres carrés,

les valeurs théoriques calculées par ce modèle, les nombres :

s'appellent les écarts des prévisions à la moyenne.

Eloignement entre un point M et une droite D dans une direction donnée :

Etant donné un point M et une droite D et un vecteur

on considère la projection m de M sur D, dans la direction du vecteur .

La distance entre les points M et m s'appelle l'éloignement du point M et de la droite D dans la direction du vecteur .

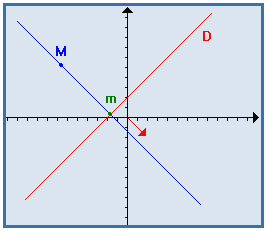
Eloignement d'un nuage de points à une droite D dans la direction de l'axe des ordonnées :

Etant donné un nuage de points et une droite D, on appelle éloignement du nuage à la droite D dans la direction de l'axe des ordonnées, la racine carrée de la moyenne des carrés des éloignements, dans la direction de l'axe des ordonnées, des points du nuage.

Eloignement d'un nuage de points à une droite D dans la direction de l'axe des abscisses :

Etant donné un nuage de points et une droite D, on appelle éloignement du nuage à la droite D dans la direction de l'axe des abscisses, la racine carrée de la moyenne des carrés des éloignements, dans la direction de l'axe des abscisses, des points du nuage.

Erreur :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

A toute valeur x_i de X est associée une valeur y_i relevée par l'observateur :

y_i est la valeur observée de la variable expliquée.

= f ( x_i ) est la valeur théorique ou valeur expliquée par le modèle.

e_i = y_i - est le résidu du modèle et

| e_i | est l'erreur du modèle.

On dit aussi que :

est la composante prévisible par le modèle et

e_i la composante imprévisible.

Inégalité de Schwarz :

Etant donné deux variables statistiques réelles X et Y, on appelle inégalité de Schwarz la relation :

| Cov ( X , Y ) | ≤ s ( X ) s ( Y )

où s ( X ) est l'écart-type de X et s ( Y ) l'écart-type de Y.

Etant donné une variable statistique réelle X prenant les n valeurs x₁, x₂, ... , x_n et une variable statistique réelle Y prenant les n valeurs y₁, y₂, ... , y_n

Cov ( X , Y ) = s ( X ) s ( Y )

si et seulement si les points du nuage :

sont alignés sur une droite à coefficient directeur positif.

Isobarycentre :

Etant donné un nuage de points , on appelle isobarycentre de ce nuage l'unique point G vérifiant :

quel que soit le point O du plan. On vérifie que :

quel que soit le point O du plan (voir point moyen).

Méthode des moindres carrés :

Etant donné un nuage de points :

il existe un modèle affine : Y = a X + b

rendant minimum la somme des carrés des résidus ( SCR ) :

Ce modèle s'obtient en prenant : a =

et en écrivant que la droite d'équation : y = a x + b passe par le point moyen du nuage : = a + b

Cov ( X , Y ) = ( x_i - ) ( y_i - )

est la covariance des variables X et Y tandis que :

s² ( X ) = ( x_i - )²

est la variance de la variable X.

Le modèle obtenu par cette méthode s'appelle l'ajustement affine de Y en X par la méthode des moindres carrés.

Modèle :

S'il existe une relation fonctionnelle entre les variables X et Y et si f est la fonction donnant pour toute valeur x de X la valeur correspondante y de Y , ( y = f ( x ) ), on dit que f est un modèle du phénomène étudié.

Moment d'inertie d'un nuage par rapport à une droite :

Etant donné un nuage de points et une droite D, on appelle moment d'inertie du nuage par rapport à la droite D la somme des carrés des distances euclidiennes des points du nuage par rapport à la droite D.

Moment d'inertie d'un nuage de points par rapport au point moyen :

Etant donné un nuage de points :

et son point moyen G,

on appelle moment d'inertie de ce nuage par rapport à G la somme des carrés des distances entre les points du nuage et G.

Nuage de points :

Soit R un repère cartésien du plan.

Si au cours de n observations ω₁, ω₂ , ... , ω_n on relève les valeurs X ( ω_i ) et Y ( ω_i ) prises par deux variables statistiques X et Y on appelle nuage de points l'ensemble des points du plan dont les coordonnées dans le repère R sont les couples ( X ( ω_i ) , Y ( ω_i ) ).

Nuage des résidus :

Etant donné un nuage de points :

et un modèle : Y = f ( X ) adapté à ce nuage.

Soient : y_i - = y_i - f ( x_i ) les résidus du modèle.

On appelle nuage des résidus associé à ce modèle le nuage de points :

Observations :

Lors d'une expérimentation, on peut être amené à différents moments, à mesurer différents paramètres liés au phénomène ou processus étudié.

Ainsi des ingénieurs relèveront la température et la longueur d'une tige d'acier à différents instants. L'ensemble de ces relevés, à un instant donné, est une observation.

Des médecins scolaires noteront pour chaque élève d'une école, leur taille et leur poids. A chaque élève est ainsi associé une observation. L'ensemble des élèves est parfois appelé aussi une population et chaque élève un individu.

Point moyen :

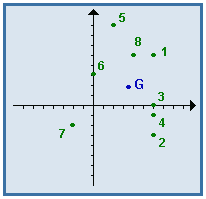
On appelle point moyen d'un nuage de points, le point dont les coordonnées sont les moyennes arithmétiques des coordonnées des points du nuage.

C'est aussi l'isobarycentre des points du nuage.

(voir isobarycentre)

Relation fonctionnelle :

Etant donné deux variables statistiques X et Y, on dit qu'il existe une relation fonctionnelle de X vers Y si à chaque valeur de la variable X est associée une valeur et une seule de la variable Y.

Résidu :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

A toute valeur x_i de X est associée une valeur y_i relevée par l'observateur :

y_i est la valeur observée de la variable expliquée.

= f ( x_i ) est la valeur théorique ou valeur expliquée par le modèle.

e_i = y_i - est le résidu du modèle.

On dit aussi que :

est la composante prévisible par le modèle et

e_i la composante imprévisible.

Somme des carrés des écarts à la moyenne ( SCT ) :

Etant donné une variable statistique réelle Y prenant les n valeurs y₁, y₂, ... , y_n, le nombre :

( y_i - )²

s'appelle la somme des écarts à la moyenne de la variable Y, ou somme des carrés totale.

Somme des carrés des écarts des prévisions à la moyenne :

Etant donné un nuage de points :

un modèle affine : Y = a X + b ajusté à ce nuage par la méthode des moindres carrés,

les valeurs théoriques calculées par ce modèle, le nombre

SCA = ( - )²

où est la moyenne des valeurs s'appelle la somme des carrés des écarts des prévisions à la moyenne.

Somme des carrés des résidus (SCR) :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

A toute valeur x_i de X est associée une valeur y_i relevée par l'observateur.

y_i est la valeur observée de la variable expliquée.

= f ( x_i ) est la valeur théorique ou valeur expliquée par le modèle.

e_i= y_i - est le résidu du modèle.

Le nombre :

s'appelle la somme des carrés des résidus ( SCR ). C'est ce nombre que l'on rend minimum lorsqu'on prend comme modèle la droite d'ajustement de Y en X par la méthode des moindres carrés.

Tableau des données brutes :

Si au cours de n observations ω₁, ω₂ , ... , ω_n on relève les valeurs X ( ω_i ) et Y ( ω_i ) prises par deux variables statistiques X et Y on appelle tableau des données brutes le tableau à deux colonnes et n lignes, où chaque ligne est réservée à une observation et chaque colonne à l'une des deux variables X ou Y.

Valeur expliquée :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

A toute valeur x_i de X est associée une valeur : = f ( x_i )

est la valeur théorique ou valeur expliquée par le modèle.

On dit aussi que est la composante prévisible.

Valeur observée :

Etant donné une variable statistique X on appelle valeur observée de cette variable, toute valeur de cette variable relevée au cours d'une observation.

Valeur théorique :

S'il existe une relation fonctionnelle entre les variables de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

A toute valeur x_i de X est associée une valeur : = f ( x_i )

est la valeur théorique ou valeur expliquée par le modèle.

On dit aussi que est la composante prévisible.

Valeurs centrées :

Soit X une variable statistique réelle prenant les valeurs : x₁ , x₂ , ... , x_n et soit la moyenne arithmétique de ces valeurs.

On appelle valeurs centrées de X les nombres :

x₁ - , x₂ - , ... , x_n -

(voir aussi écart à la moyenne, variable statistique centrée).

Valeurs centrées réduites :

Soit X une variable statistique réelle prenant les valeurs : x₁ , x₂ , ... , x_n et soit la moyenne arithmétique de ces valeurs.

s ( X ) l'écart-type de X.

On appelle valeurs centrées réduites de X les nombres :

(voir aussi variable statistique centrée réduite).

Variable explicative :

S'il existe une relation fonctionnelle entre les variables X et Y de X vers Y et si f est un modèle de cette relation ( Y = f ( X ) ) on dit que X est la variable explicative et Y la variable expliquée.

Variable expliquée :

Variable statistique centrée :

Soit X une variable statistique et sa moyenne.

On appelle variable statistique centrée la variable X -

(voir aussi écarts à la moyenne, valeurs centrées)

Variable statistique centrée réduite :

Si X est une variable statistique réelle, la variable

où est la moyenne de la variable X et s ( X ) son écart-type, s'appelle la variable centrée réduite associée à X.

(voir aussi valeurs centrées réduites)

Variable statistique réelle :

L'application de l'ensemble Ω des observations dans qui à chaque observation ω associe la mesure X ( ω ) d'une grandeur X relevée au cours de cette observation s'appelle une variable statistique réelle.

Variance :

Etant donné une variable statistique réelle X prenant les n valeurs x₁ , x₂ , ... , x_n , le nombre

s² ( X ) = 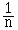( x_i - )²

est la variance de la variable X. Pour calculer la variance on peut utiliser la formule de Huyghens :

Variance des prévisions :

Etant donné un nuage de points :

un modèle affine : Y = a X + b ajusté à ce nuage par la méthode des moindres carrés,

les valeurs théoriques calculées par ce modèle, le nombre

où est la moyenne des valeurs s'appelle la variance expliquée par l'ajustement ou variance des prévisions.

Variance des valeurs observées :

Etant donné un nuage de points :

le nombre :

s'appelle la variance des valeurs observées ou variance totale.

Variance expliquée :

Etant donné un nuage de points :

un modèle affine : Y = a X + b ajusté à ce nuage par la méthode des moindres carrés,

les valeurs théoriques calculées par ce modèle, le nombre

où est la moyenne des valeurs s'appelle la variance expliquée par l'ajustement ou variance des prévisions.

Variance résiduelle :

Etant donné un nuage de points :

un modèle affine : Y = a X + b ajusté à ce nuage par la méthode des moindres carrés,

les valeurs théoriques calculées par ce modèle, le nombre

s'appelle la variance résiduelle.

Variance totale :

Etant donné un nuage de points :

le nombre :

s'appelle la variance des valeurs observées ou variance totale.

Vecteur directeur

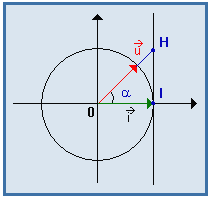
Etant donné une droite D,

un vecteur non nul est un vecteur directeur de la droite D

si pour tout point M de la droite D il existe un scalaire λ tel que :