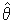 d'un paramètre θ est sans biais si son espérance est égale à θ .
d'un paramètre θ est sans biais si son espérance est égale à θ . LEXIQUE :
Choisissez le terme à expliquer...Un estimateur 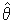 d'un paramètre θ est sans biais si son espérance est égale à θ .
d'un paramètre θ est sans biais si son espérance est égale à θ .
Par exemple la moyenne ![]() calculée sur un échantillon aléatoire simple est un estimateur sans biais de
la moyenne m de la population. Sinon, le biais d'un estimateur
calculée sur un échantillon aléatoire simple est un estimateur sans biais de
la moyenne m de la population. Sinon, le biais d'un estimateur 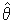 est la valeur de E (
est la valeur de E ( 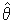 ) - θ.
) - θ.
Un biais positif signifie que l'estimation, en moyenne, surestime θ, alors qu'un biais négatif le sous-estime.
On dit qu'une variable aléatoire X est centrée (ou que sa loi est centrée) si son espérance est nulle : E ( X ) = 0.
On dit que l'on centre une variable aléatoire X quand on lui ôte sa moyenne : X - E ( X ) est une variable centrée.
Si X n'est pas constante, ![]() est une variable centrée réduite.
est une variable centrée réduite.
Pour une variable aléatoire X, c'est ![]() , qui vaut 3 dans le cas gaussien.
, qui vaut 3 dans le cas gaussien.
Pour un échantillon, c'est ![]() , qui est > 3 dans le cas
, qui est > 3 dans le cas
d'une distribution moins aplatie que la loi de Gauss,
et < 3 dans le cas contraire.
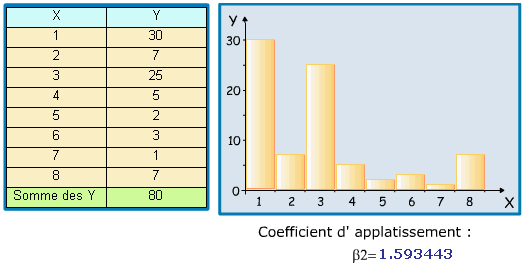
Coefficient de corrélation linéaire :
Etant donné une variable statistique réelle X prenant les n valeurs x1 , x2 , ... , xn et une variable statistique réelle Y prenant les n valeurs y1 , y2 , ... , yn , le nombre
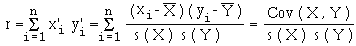
s'appelle le coefficient de corrélation linéaire des variables X et Y.
Coefficient de détermination :
Etant donné une variable statistique réelle X prenant les n valeurs x1 , x2 , ... , xn et une variable statistique réelle Y prenant les n valeurs y1 , y2 , ... , yn , le nombre
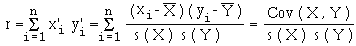
s'appelle le coefficient de corrélation linéaire des variables X et Y.
Le nombre : R = r² = ![]()
s'appelle le coefficient de détermination des variables X et Y.
Pour une variable aléatoire X, c'est ![]() ,
qui vaut 0 si la loi de X est symétrique (notamment pour une loi de Gauss).
,
qui vaut 0 si la loi de X est symétrique (notamment pour une loi de Gauss).
Pour un échantillon, c'est ![]() , coefficient sans unité, nul dans le cas d'une distribution symétrique,
positif si elle est étalée à droite, négatif si elle est étalée à gauche.
, coefficient sans unité, nul dans le cas d'une distribution symétrique,
positif si elle est étalée à droite, négatif si elle est étalée à gauche.
a) de la loi binomiale vers la loi de Poisson :
Si X suit B ( n , p ) , n → ∝ , p → 0, np → λ , alors la loi de X se rapproche de P ( λ ).
(en pratique, si n > 50 et p < 0.1, on peut remplacer B ( n , p ) par P ( n p ))
b) de la loi binomiale vers la loi normale :
Si X suit B ( n , p ), quand n → ∝ ,
![]() tend vers la loi N ( 0 , 1 ).
tend vers la loi N ( 0 , 1 ).
(en pratique, si np > 18 et p assez proche de 0.5, on peut remplacer la loi de X
par N ( n p ; ![]() )
)
c) de la loi de Poisson vers la loi normale :
Si X suit P ( λ ) , ![]() tend, quand λ → ∝ , vers la loi N (0, 1)
tend, quand λ → ∝ , vers la loi N (0, 1)
(en pratique, si λ > 18 , on peut remplacer la loi de X
par N ( λ , ![]() ) )
) )
C'est la représentation graphique du risque de seconde espèce β, fonction du paramètre à tester θ, lorsque H1 est composite.
Diagramme quantile-quantile, ou QQ plot, ou droite de Henry :
Diagramme représentant la fonction de répartition empirique, gradué en ordonnée selon les fractiles de la loi normale centrée réduite, ce qui fait que si Fn est proche de la fonction de répartition d'une loi de Gauss, les points sont presque alignés, le long d'une droite appelée droite de Henry.
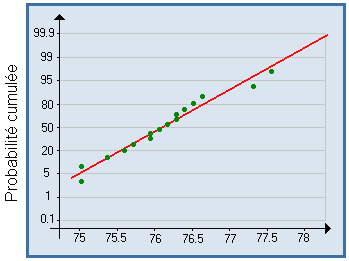
Données appariées : (ou échantillons appariés)
C'est le cas où on dispose de 2 séries de mesures, portant sur le même échantillon :
Exemples :
- mesures biologiques sur des individus, avant et après un traitement ;
- double correction des mêmes copies ;
- rendements obtenus par deux variétés cultivées sur des
couples de parcelles voisines, etc...
L'écart-type d'une variable aléatoire numérique X, noté σ ( X ), est la racine carrée de la variance.
L'écart-type s'exprime dans la même unité que X ; c'est un nombre positif ou nul, nul si X est une constante, et d'autant plus grand que les valeurs de X sont "imprévisibles".
Exemple : si X suit une loi normale, la probabilité pour que X soit compris entre E ( X ) - 2 σ ( X ) et E ( X ) + 2 σ ( X ) est à peu près de 0.95.
Echantillon : (ou Echantillonnage)
Echantillon obtenu par tirages équiprobables et indépendants de n éléments d'une population : chaque individu a la même probabilité d'être tiré, et ceci de façon indépendante d'un individu aux suivants (tirage dit "avec remise").
Ce terme désigne aussi :
- une suite de n variables aléatoires indépendantes de même loi de probabilité ( X1 , X2 , ... , Xn )
- la réalisation de cette suite de variables : ( x1 , x2 , ... , xn )
Par exemple l'échantillon peut être 100 personnes choisies au hasard parmi la population d'une ville, ou les salaires de ces 100 personnes, ce peut être de même un échantillon de 50 pièces fabriquées par une machine, ou les diamètres de ces 50 pièces, ou les poids de ces 50 pièces, etc....
L'espérance (mathématique) d'une variable aléatoire numérique X, appelée aussi parfois par abus de langage moyenne de X, est la valeur
que l'on peut espérer obtenir, en moyenne, en réalisant X.
Elle est notée E ( X ).
a) dans le cas d'une variable X discrète, de loi de probabilité définie par les xi et les pi , c'est la moyenne des xi , pondérée par les pi
E ( X ) = ∑ ( xi pi )
b) dans le cas d'une variable X continue, de fonction de densité f, c'est l'intégrale, sur l'intervalle des valeurs de X, de la fonction x f ( x ) :
E ( X ) = ∫ x f ( x ) d x
Variable aléatoire, fonction de variables d'échantillon X1 , X2 , ... , Xn dont la réalisation est une estimation (c'est-à-dire une valeur approchée) d'un paramètre θ inconnu de la population.
Par exemple : ![]()
est un estimateur de m, moyenne de la population (m = E ( X ) ). Sa réalisation est ![]() , moyenne calculée sur l'échantillon.
, moyenne calculée sur l'échantillon.
On dit que l'on procède à une estimation par intervalle d'un paramètre θ lorsqu'on détermine un intervalle de confiance pour θ.
C'est une valeur approchée 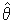 du paramètre θ inconnu d'une population, calculée à partir d'un échantillon.
du paramètre θ inconnu d'une population, calculée à partir d'un échantillon.
C'est en fait la réalisation d'une variable aléatoire 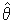 , estimateur de θ.
, estimateur de θ.
Par exemple le % de votants obtenus pour M. Truc lors d'une élection, sur 1 000 bulletins dépouillés au hasard, est une estimation du % de voix de M. Truc.
C'est l'hypothèse, notée H1, qui sera retenue si l'hypothèse nulle H0 est rejetée.
C'est une hypothèse de la forme :
où θ est un paramètre inconnu dont on veut tester la valeur,
et θ0 une valeur numérique fixée.
C'est l'hypothèse, notée H0, concernant une population, que l'on confronte au résultat d'observations sur échantillon(s), elle peut concerner par exemple la valeur d'un paramètre, ou bien le type de loi suivie par une variable aléatoire.
C'est une hypothèse ( H0 ou H1 ) de la forme
θ = θ0 ,
où θ est un paramètre inconnu dont on veut tester la valeur,
et θ0 une valeur numérique fixée.
Deux variables aléatoires X et Y sont indépendantes si la connaissance de la réalisation d'un événement lié à l'une des deux ne modifie pas les probabilités d'événements liés à l'autre.
a) Si X et Y sont discrètes, elles sont indépendantes si et seulement si
P ( X = xi et Y = yj ) = P ( X = xi ) . P ( Y = yj ),
pour tout xi de ![]() et tout yj de
et tout yj de 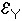 .
.
b) Si X et Y sont continues, elles sont indépendantes si et seulement si la fonction de densité du couple ( X , Y ) est le produit des densités marginales.
Intervalle de confiance : (de niveau 1 - α)
Un intervalle de confiance de niveau 1 - α pour un paramètre inconnu θ d'une population est un intervalle tel que la probabilité pour que θ appartienne à cet intervalle est 1 - α. Les bornes de cet intervalle se calculent à partir d'un échantillon.
Par exemple, si M. Truc obtient 40 % des voix sur un échantillon aléatoire simple de 1 000 votants, on peut dire, avec une probabilité de 0.95,
que le % de votants pour M. Truc se situe entre 37 % et 43 %.
[37 43] est un intervalle de confiance de niveau 0.95 pour le % de votants pour M. Truc.
C'est la loi de X = nombre de réalisations d'un événement dans une suite de n épreuves indépendantes où l'événement a la probabilité p de se produire.
X est la somme de n variables de Bernoulli indépendantes de même p :
![]() = {0 , 1 , 2 , ... , n}
= {0 , 1 , 2 , ... , n}
![]() ∀ k ∈ { 1 , 2 , ... , n }
∀ k ∈ { 1 , 2 , ... , n }
E ( X ) = np V ( X ) = np ( 1 - p )
Exemples :
- nombre de "pile" obtenu en lançant 10 fois une pièce : B (10 ; 0.5)
- nombre de pièces défectueuses trouvées parmi 100 ...
C'est la loi d'une variable aléatoire continue positive définie comme étant le rapport de deux variables
de 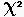 indépendantes, chacune divisée par son nombre de degrés de liberté :
indépendantes, chacune divisée par son nombre de degrés de liberté :
( voir Tables )
Une variable aléatoire X suit une loi du 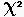 à n
degrés de liberté si X est égale à la somme des carrés de n variables aléatoires indépendantes de loi normale centrée réduite.
Cette loi est tabulée ( voir Tables ).
à n
degrés de liberté si X est égale à la somme des carrés de n variables aléatoires indépendantes de loi normale centrée réduite.
Cette loi est tabulée ( voir Tables ).
a) X suit une loi normale centrée réduite, notée N (0, 1), si sa fonction de densité est :
![]()
Sa fonction de répartition se lit dans une table.
b) X suit une loi normale de paramètres m et σ , notée N ( m , σ ), si sa fonction de densité est :
![]()
![]() suit alors une loi normale centrée réduite.
suit alors une loi normale centrée réduite.
On dit aussi que X suit une loi de Gauss ou une loi de Laplace-Gauss.
C'est la loi d'une variable X à valeurs dans N telle que
Si X suit une loi binomiale B ( n , p ) avec p faible ( < 0, 1 ), et n grand ( n > 50), la loi de X est très proche de la loi P ( n p ).
Exemple : nombre de pièces défectueuses dans un grand échantillon de bonne qualité.
C'est aussi la loi du nombre d'événements se produisant pendant une période T, ou sur une distance T,
et ne dépendant que de T, les événements étant indépendants, et non simultanés.
Exemple : nombre d'accidents par an sur une route, nombre de défauts par mètre de tissu, nombre d'appels téléphoniques reçus à un standard pendant une journée.
Si X suit une loi P ( λ ), E ( X ) = V ( X ) = λ
Une variable aléatoire X suit une loi de Student à n degrés de liberté si
X est de la forme : ![]()
où U et Y sont indépendantes, U de loi N
(0, 1) et Y de loi 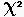 ( n ).
( n ).
Cette loi est tabulée ( voir Tables ).
Elle peut s'exprimer de deux façons :
1) Lorsqu'on effectue un échantillonnage aléatoire simple, la fréquence d'apparition d'un événement
F tend, quand la taille n de l'échantillon tend vers l'infini, vers la proportion p
dans la population-mère.
Par exemple, si l'on pouvait jouer indéfiniment à "pile ou face" avec une pièce bien équilibrée, le pourcentage
de "pile" obtenu tendrait vers 50 %.
2) De même, la moyenne d'une variable sur un échantillon aléatoire simple tend, quand n tend vers l'infini, vers la moyenne dans la population.
Par exemple, la taille moyenne de n enfants de 10 ans pris au hasard dans la population française tend, si n tend vers l'infini, vers la taille moyenne de tous les enfants français de 10 ans.
Moyenne (variance , écart-type) émpirique :
C'est la moyenne (variance, écart-type) calculée sur les valeurs obtenues dans l'échantillon.
C'est en fait la réalisation d'une variable aléatoire :
la moyenne empirique : ![]() est la réalisation de :
est la réalisation de :
![]() , que l'on appelle aussi moyenne empirique.
, que l'on appelle aussi moyenne empirique.
C'est 1 - α, où α est le risque de 1 ère espèce. C'est la probabilité d'accepter à juste titre une hypothèse H0 vraie.
Ensemble bien défini de personnes, ou d'objets, sur lesquels on effectue des mesures (population formée des habitants d'une ville, ou des communes d'un pays, ou des entreprises d'une région, ou des pièces fabriquées par une machine, ou des boîtes de conserves d'un magasin, etc...).
Les mesures peuvent être effectuées sur la population toute entière, ou seulement sur une partie d'entre elle, appelée échantillon.
Probabilité critique : (ou niveau de dépassement, ou niveau de signification)
C'est la probabilité d'obtenir pour la variable de décision T d'un test une valeur au moins aussi éloignée que la valeur obtenue t
sur échantillon(s), lorsque H0 est vraie.
Cette valeur p , fournie par la plupart des logiciels de tests, comparée au risque α de première espèce qu'on accepte de prendre permet de conclure :
si p ≤ α , on rejette H0
si p > α , on garde H0
C'est la valeur (ou la fonction si H1 est composite) P = 1 - β, où β est le risque de 2ème espèce du test.
C'est la probabilité de rejeter H0 lorsqu'elle est effectivement fausse.
On dit qu'une variable aléatoire X est réduite (ou que sa loi est réduite) si sa variance est égale à 1 (et donc son écart-type aussi) : V ( X ) = 1
On dit que l'on réduit une variable aléatoire X (non constante) quand on la divise par son écart-type :
![]() est une variable réduite,
est une variable réduite,
![]() est une variable centrée réduite.
est une variable centrée réduite.
C'est  , le complémentaire de la région critique.
, le complémentaire de la région critique.
Elle est telle que, si H0 est vraie :
P ( T ∈  ) = 1 - α , où
α est le risque de 1ère espèce.
) = 1 - α , où
α est le risque de 1ère espèce.
Région critique (ou région de rejet) :
C'est le domaine W des valeurs de la variable de décision t conduisant à rejeter H0.
Elle est telle que, si H0 est vraie, P ( T ∈ W ) = α , risque de 1ère espèce.
C'est la règle de construction d'un test qui, après échantillonnage, nous permet de conclure si on accepte ou non l'hypothèse H0.
Cette règle doit être établie avant de confronter les données expérimentales à l'hypothèse à tester.
C'est la probabilité α de rejeter à tort une hypothèse H0 vraie, lors d'un test statistique : c'est la probabilité de se tromper, en déclarant fausse une hypothèse nulle qui en fait est vraie.
Ce risque est généralement fixé à l'avance, de l'ordre de 0.01 à 0.05.
C'est la probabilité β d'accepter à tort une hypothèse H0, lors d'un test statistique : c'est la probabilité de se tromper en déclarant vraie l'hypothèse nulle H0, alors que c'est en fait l'hypothèse alternative H1 qui est vraie.
Si H1 est composite, β est une fonction du paramètre.
On dit qu'un test est robuste s'il reste valable même si les suppositions faites sur la population pour le construire ne sont pas toutes exactement vraies :
c'est notamment le cas de l'hypothèse de normalité dans la population.
Tableau résultant du tri croisé de deux variables.
| Y | ||||||||||||||||
| X |
|
Nombre n d'éléments de l'échantillon.
Par exemple un échantillon de 1 000 électeurs est un échantillon de taille 1 000.
Test non paramétrique où H0 concerne le type de loi de probabilité suivie par X dans la population.
Il s'agit de comparer une distribution observée sur échantillon à une distribution théorique.
C'est un test de comparaison de deux moyennes sur la base de 2 échantillons indépendants de tailles n1
et n2, issus de lois normales, où les variances ![]() et
et ![]() sont inconnues et inégales ( ceci étant vérifié par un test F ).
sont inconnues et inégales ( ceci étant vérifié par un test F ).
Le test est basé sur ![]() qui suit approximativement , sous H0,
une loi de Student à ν degrés de liberté, où ν est l'entier le plus proche tel que :
qui suit approximativement , sous H0,
une loi de Student à ν degrés de liberté, où ν est l'entier le plus proche tel que :
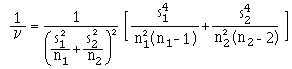
C'est un test paramétrique où H1 est de la forme :
θ ≠ θ0, dans le cas d'un test de signification,
ou bien de la forme :
θ1 ≠ θ2 dans le cas d'un test de comparaison.
Test basé sur les valeurs θ1 et θ2 des paramètres de 2 populations, inconnus. Sur la base de 2 échantillons issus de ces 2 populations, on veut tester H0 :
θ1 = θ2
On ne cherche pas à tester la valeur numérique de θ1 et θ2 , on veut seulement savoir s'ils sont égaux.
Test d'hypothèse statistique :
Procédure basée sur une fonction d'échantillon(s), conduisant à accepter ou à rejeter une hypothèse H0 concernant la population dont est issu l'échantillon.
Test d'indépendance (ou d'homogénéité) :
C'est un test non paramétrique où H0 est l'hypothèse selon laquelle X et Y ( sur la même population ) sont indépendantes.
Il s'agit de comparer l'observation simultanée de X et Y sur un échantillon à leur répartition théorique sous hypothèse d'indépendance.
Test d'ajustement d'une répartition empirique à une loi théorique sur k classes s'effectue en comparant :
![]()
à ![]() , pour un nombre de degrés de liberté égal à :
, pour un nombre de degrés de liberté égal à :
k - 1 - nombre de paramètres estimés sur l'échantillon.
H0 est rejetée si ![]() >
> ![]() , au niveau 1 - α.
, au niveau 1 - α.
Test de khi-deux d'indépendance (ou d'homogénéité)
Test d'indépendance entre 2 variables X et Y à K et L catégories, mesurées sur n individus, basé sur la comparaison de
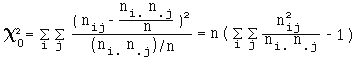
à ![]() à ( K - 1 ) ( L - 1 ) degrés de liberté.
à ( K - 1 ) ( L - 1 ) degrés de liberté.
On accepte l'hypothèse d'indépendance, au niveau 1 - α , si ![]() <
< ![]()
Test de Kolmogorov (pour un échantillon)
Test d'ajustement d'une répartition empirique continue à une répartition théorique, basé sur l'écart maximum entre les 2 répartitions :
![]()
qui doit être inférieur à une valeur lue dans la table pour que H0 soit acceptée.
Test de Kolmogorov-Smirnov (pour 2 échantillons indépendants)
Test de comparaison de la distribution de 2 variables, à partir de 2 échantillons indépendants, basé sur l'écart maximum entre leurs fonctions de répartition empiriques, comparé à une table.
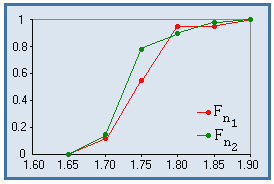
Pour n1 et n2 ≥ 30, on compare d à la valeur critique maximale
![]() , où C
prend les valeurs suivantes en fonction de α :
, où C
prend les valeurs suivantes en fonction de α :
| Test bilatéral | Test unilatéral | |
| α = 5 % | 1.36 | 1.22 |
| α = 1 % | 1.63 | 1.52 |
Test de comparaison de 2 proportions, dans le cas de 2 échantillons appariés : les mêmes n individus sont répartis selon 2 critères dichotomiques :
| Question 2 | |||||||||||||||||
| Question 1 |
|
Le test de comparaison de ![]() à
à ![]() est basé sur :
est basé sur :
![]() , qui suit sous H0
une loi de
, qui suit sous H0
une loi de 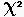 à 1 degré de liberté :
à 1 degré de liberté :
si cette quantité est inférieure
au quantile 1 - α de la loi de 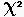 ( 1 ), on accepte l'hypothèse d'égalité des fréquences
de "oui" aux 2 questions.
( 1 ), on accepte l'hypothèse d'égalité des fréquences
de "oui" aux 2 questions.
Se dit de tout test d'hypothèse qui n'est pas un test paramétrique : cela peut être un test d'adéquation, d'indépendance, ou autre.
C'est un test portant sur la valeur d'un ( ou de plusieurs ) paramètre(s) d'une population ; ou sur la comparaison des paramètres de 2 populations.
H0 est de la forme : θ = θ0 , ou bien : θ1 = θ2
Test de normalité basé sur la comparaison à 1 de W0, coefficient de détermination entre les valeurs xi d'un échantillon et des coefficients centrés réduits ai : si W0 est suffisamment proche de 1, on accepte l'hypothèse selon laquelle l'échantillon est issu d'une loi normale.
W0 est toujours compris entre 0 et 1.
Test de signification (ou test de comparaison à une norme) :
Test basé sur la valeur θ d'un paramètre d'une population, où H0 est :
θ = θ0
θ0 étant une valeur numérique fixée ( une "norme" )
C'est un test paramétrique où l'hypothèse H1 est de la forme :
θ > θ0, ou θ < θ0 dans le cas d'un test de signification,
ou bien de la forme :
θ1 > θ2 ou θ1 < θ2 dans le cas d'un test de comparaison.
C'est le test de comparaison de deux variances de l'hypothèse
H0 : ![]() =
= ![]() ,
basé sur la valeur de
,
basé sur la valeur de ![]() qui suit une loi de Fisher à
qui suit une loi de Fisher à
n1 - 1 , n2 - 1 degrés de liberté sous H0.
![]() et
et ![]() sont les estimateurs sans biais de
sont les estimateurs sans biais de ![]() et
et ![]() et les 2 échantillons sont issus de lois normales.
et les 2 échantillons sont issus de lois normales.
Test T : (pour un échantillon)
Test effectué pour tester la moyenne inconnue m d'une population lorsque l'écart-type σ est inconnu.
Ce test est basé sur T = ![]() qui suit une loi de Student ( n - 1 )
qui suit une loi de Student ( n - 1 )
si l'hypothèse H0 : m = m0 est vraie.
Test T de comparaison (ou d'égalité) de 2 moyennes :
C'est un test d'égalité des moyennes m1 et m2
de 2 populations sur la base de 2 échantillons indépendants lorsque l'écart-type des deux
populations ( σ1 et σ2 ) est inconnu
mais où on peut considérer que
σ1 = σ2, et que les variables sont normales.
On teste H0 : m1 = m2 contre H1 : m1 ≠ m2 ou m1 < m2 ou m1 > m2
Le test est basé sur 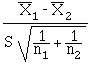 qui suit, si H0
est vraie, une loi de Student à n1 + n2 - 2 degrés de liberté,
qui suit, si H0
est vraie, une loi de Student à n1 + n2 - 2 degrés de liberté,
avec : 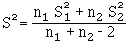
Test de Wilcoxon pour des données appariées
A partir de 2 séries de mesures de variables continues, X et Y, sur les mêmes individus, on note la somme des rangs des différences xi - yi positives, dans l'interclassement des n différences par ordre croissant de valeur absolue.
Connaissant, sous H0 ( X et Y de même loi ), l'espérance et la variance de cette somme, à peu près gaussienne si n ≥ 20, on en déduit les valeurs critiques :
Test non paramétrique de comparaison de 2 échantillons indépendants, de lois continues, basé sur la somme des rangs occupés par les éléments
d'un échantillon dans l'interclassement des 2 échantillons regroupés : connaissant sous H0
(égalité des 2 lois) l'espérance et la variance de cette somme, de loi à peu près gaussienne, on
en déduit les valeurs critiques du test. Si n1 et n2
sont les tailles d'échantillons, la somme des rangs du premier a, sous H0,
pour espérance : ![]() et pour variance :
et pour variance : ![]()
Test effectué pour tester la moyenne inconnue m d'une population lorsque l'écart-type σ est connu.
Ce test est basé sur 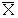 qui suit une loi :
qui suit une loi :
N ( m ; ![]() )
si l'hypothèse H0 : m = m0 est vraie.
)
si l'hypothèse H0 : m = m0 est vraie.
Test Z de comparaison (ou d'égalité) de 2 moyennes :
C'est un test d'égalité des moyennes m1 et m2 de 2 populations sur la base de 2 échantillons indépendants lorsque l'écart-type des deux populations ( σ1 et σ2 ) est connu.
On teste H0 : m1 = m2 contre H1 : m1 ≠ m2 ou m1 < m2 ou m1 > m2
Le test est basé sur ![]() qui suit, si H0 est vraie, une loi :
qui suit, si H0 est vraie, une loi : ![]()
( n1 et n2 sont les tailles d'échantillons).
Les populations suivent des lois normales où n1 et n2 sont ≥ 5.
Test Z de comparaison (ou d'égalité) de 2 proportions :
C'est un test d'égalité de proportions p1 et p2 dans 2 populations sur la base de 2 échantillons indépendants de taille n1 et n2.
On teste H0 : p1 = p2 contre H1 : p1 ≠ p2 ou p1 < p2 ou p1 > p2
Le test est basé sur la différence des fréquences F1 - F2 qui suit à peu près, si H0 est vraie, une loi :
où f est la fréquence sur la réunion des deux échantillons :
Si X1, X2, X3, ... , Xn sont des variables aléatoires indépendantes, de même loi de probabilité, d'espérance µ et de variance σ², la loi de probabilité de :
tend, quand n → ∝, vers la loi normale centrée réduite.
Valeur c telle que ( pour un test paramétrique unilatéral ) la décision d'accepter ou de rejeter H0 est fonction de la position de la variable de décision t par rapport à c.
C'est une fonction T de l'échantillon X1, X2 , ... , Xn, donc une variable aléatoire, dont la valeur observée permet de conclure un test statistique.
T est choisie de telle sorte que, si H0 est vraie, sa loi de probabilité est parfaitement connue.
La variance d'une variable aléatoire numérique X, notée V ( X ), est un nombre positif ou nul, nul si X est une constante, et d'autant plus grand que les valeurs de X sont "imprévisibles".
V ( X ) = E [ ( X - E ( X ) )2 ] (ici E signifie l'espérance)
On a aussi : V ( X ) = E ( X2 ) - [ E ( X ) ]2 , formule qui peut se lire : la variance est égale à l'espérance du carré moins le carré de l'espérance.
La racine carrée de la variance est l'écart-type.